OpenKnowledge Logo Manual

What is OpenKnowledge?

Suppose you want to get something complex done using components (such as Web services) that are available on the Internet. You could write your own Web service, that calls out to those other components, and host that on your own system but that will only work for you alone. What if you think others might benefit from coordinating in a similar way, or if you want to avoid always having your system perform the coordination? That's where OpenKnowledge comes in. It provides you with a compact language for describing coordination and, if you wish to do so, a means of sharing coordination with others. The "world view" taken by OpenKnowledge is illustrated in the picture below, where the different coloured arrows represent people (or automated systems) participating in different interactions. Each interaction is coordinated by a model of the interaction, discussed later. An individual gains knowledge of how to interact with other individuals through interacting with those who he or she already knows. For example, in the picture below the individual on the left might initially know about only two other individuals (the two interacting via the light green arrows) but those two individuals know about other interactions (in dark blue and in lime green) so can communicate them to the individual on the left.

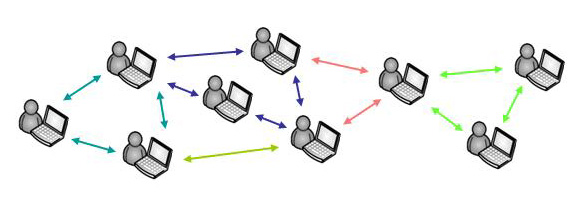
Shared interactions

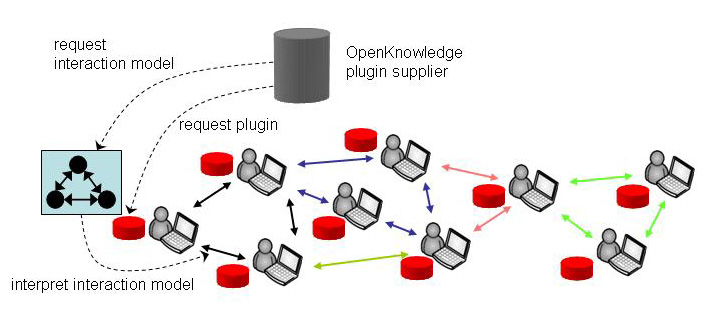
Interaction models are can be shared and used in many different ways but the standard way to use them is by downloading the OpenKnowledge kernel system from www.openk.org. The kernel is a compact program that automatically finds interaction models that you might want to use; allows you to subscribe to interactions that interest you; and interprets the interaction models in which you actually become involved. In the illustration below, the red dots are copies of the kernel system (loaded from the supplier) being run on individual peers.

Bootstrapping

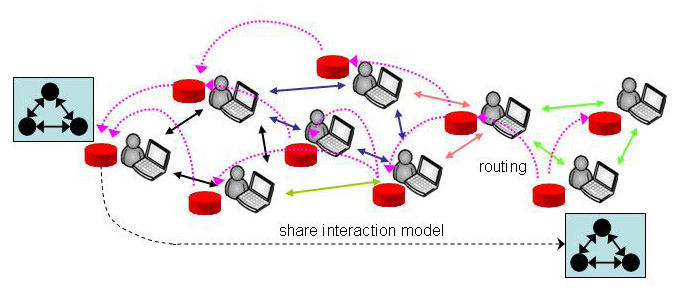
Although our interaction models are portable and could be used by different systems, there is a social advantage in having many peers running the same OpenKnowledge kernel. The social advantage comes from query routing, which works roughly as shown in the picture below. Suppose that the peer at bottom right of the picture wants to undertake an interaction but does not have an appropriate interaction model. That peer would describe the sort of interaction he or she is seeking, using a sequence of keywords (in a similar way to the way you search for Web pages in traditional Web browsers). This query then is routed through the peer network until matching interaction models are found (in our picture the interaction model in black matches the query) and are relayed back to the peer. When the peer receives the interaction model it receives not only the interaction but, through it, may also access other peers in the network with which it may not previously have interacted. In this way, sharing interaction models extends and reinforces social networks. Routing

If you want simply to use interaction models then you do not need to understand any technical detail of the underlying system because using an interaction model is analogous to using a program - if the interaction model is well crafted then it will be easy for an appropriate group of people to use without them knowing how it is built. You may, however, want to write your own interaction models or adapt those you find on the network. This is the topic of the next section. If you want a broader view of the objectives of OpenKnowledge then you should read the Openknowledge manifesto. For a more technical overview of LCC please refer to the LCC overview paper.

Writing Your Own LCC Interactions

This section explains how to write your own interaction models, which you can then use and share with others. We begin with a basic example.

Syntax

Each LCC interaction model is defined by a set of clauses where each clause has the following syntax (in BNF form).
Clause := Role :: Def
Role := a(Type, Id)
Def := Role | Message | Def then Def | Def or Def
Message := M => Role | M => Role <-- C | M <= Role | C <-- M <= Role
C := Constant | P(Term,...) not(C) | C and C | C or C
Id := Constant | Variable
Term := Constant | Variable | P(Term,...)
Type := Term
M := Term
P := Constant
Constant := Character sequence beginning with an lower case character | number
Variable := Character sequence beginning with an upper case character
Each clause is a self contained definition of a role, with message passing being the only means of transferring information between roles. Message passing is also the only means of synchronisation between roles.

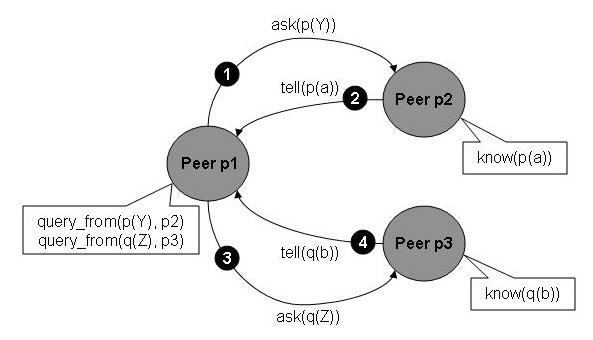
A Basic Example

The diagram below shows an interaction between three peers: p1, p2 and p3. Each peer knows different things: The interaction we require is depicted by the numbered messages in the diagram: Basic example

Let us first define an interaction model that does exactly the message passing defined above. There are two roles that agents take in this model: the role of a requester (which asks for information) and the role of an informer (which supplies information). We define a LCC clause for each role as shown below. For the requester (p1) we have simply given the sequence of four messages corresponding to those above. Then we have defined a clause for the role of informer that defines the behaviour expected of p2 and p3. 

a(requester, A) ::
    ask(X1) => a(informer, p2) <-- query_from(X1, p2) then
    tell(X1) <= a(informer, p2) then
    ask(X2) => a(informer, p3) <-- query_from(X2, p3) then
    tell(X2) <= a(informer, p3)

a(informer, B) ::
    ask(X) <= a(requester, B) then
    tell(X) => a(requester, B) <-- know(X).

The LCC definition above covers the example but suppose we want a more general type of requester that takes a list, L, of the form [q(Query,Peer),..,], where Query is the query we want to make and Peer is an identifier for the peer to which we want to send the query. We want the requester to send an ask(Query) message to the appropriate Peer for each query and receive a tell(Query) reply each time. A standard way to do this is by giving L as a parameter to the requester role (so it becomes requester(L)) and making the definition of this role recursive, taking the first element of L and then applying the same definition to the remainder of the list, Lr, as shown below. 

a(requester(L), A) ::
    (  ask(Query) => a(informer, Peer) <-- L = [q(Query,Peer) | Lr] then
       tell(Query) <= a(informer, Peer) then
       a(requester(Lr), A)  )
    or
    null <-- L = [].

a(informer, B) ::
    ask(X) <= a(requester(_), B) then
    tell(X) => a(requester(_), B) <-- know(X).

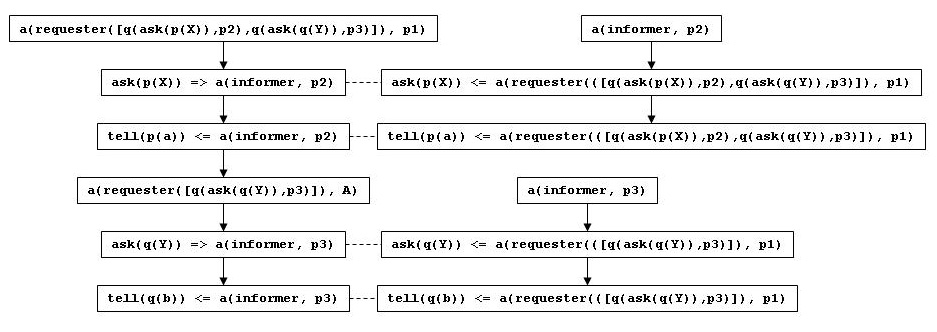
If we were to run the interaction model shown below, starting with the role of requester for the list of queries [q(ask(p(X)),p2),q(ask(q(Y)),p3)], then we get the message sequences shown below. On the left is the sequence for a(requester([q(ask(p(X)),p2),q(ask(q(Y)),p3)]), p1). On the right are the sequences for a(informer, p2) and a(informer, p3) which are the roles undertaken by p2 and p3 in response to p1. The dashed lines indicate synchronisation via message passing between peers. Event sequences

Design Patterns

Perhaps the easiest way to understand LCC programming is through design patterns. These are standard ways of structuring clauses that are used to obtain specific forms of interaction. The broad idea is similar to design patterns in more traditional languages but the good news for LCC is that you only need to know a small number of patterns, which you then combine to make more complex programs. The four key patterns are given below.

Pattern 1: Interaction

The simplest thing we can do with LCC is to specify a message being sent from one peer to another. To do this we decide the role (r1) being taken by the sender; then write M => a(r2, Y) <-- C to describe the message, M, being sent out to the recipient, Y, which is expected to receive it in role r2. The constraint C1 is used to determine whether this message can be sent by the sender, and it often is used also to determine values for any variables that appear in M. In the specification of the recipient's role we write C2 <-- M <= a(r2, X) to describe the message, M, being received, with C2 giving a constraint that should hold as a consequence of receiving it. 
a(r1, X) ::
    ...
    M => a(r2, Y) <-- C1
    ...

a(r2, Y) ::
    ...
    C2 <-- M <= a(r2, X)
    ...
An example of using this pattern is an interaction that sends a message, M, to a recipient, Y, where the choice on M is made by the constraint message(M) and the choice of recipient is made by the constraint recipient(Y). Acceptance of the message by the recipient is determined by the constraint accept(M). 
a(sender, X) ::
    M => a(recipient, Y) <-- message(M) and recipient(Y)

a(recipient, Y) ::
    accept(M) <-- M <= a(sender, X)

Pattern 2: Sequence

Usually we want to put an ordering on the sequence of events that can occur as part of a role. To do this we use the "then" operator to say that the earlier event, E1, comes before the later event, E2. 
a(r, X) ::
    ...
    E1 then
    E2
    ...
An example that uses this pattern twice is when the recipient of the message returns a message to the sender, where response(M1, M2) is a constraint determining the recipient's response message, M2, from the sender's message, M1. 
a(sender, X) ::
    M1 => a(recipient, Y) <-- message(M1) and recipient(Y) then
    accept(M2) <-- M2 <= a(recipient, Y)

a(recipient, Y) ::
    accept(M1) <-- M1 <= a(sender, X) then
    M2 => a(sender, X) <-- response(M1, M2)

Pattern 3: Choice

We may want a peer taking some role, r, in an interaction to make a choice about the course of its interaction with other peers. This is done by writing E1 <-- C1 or E2 <-- C2 to say that the interaction described by E1 should be done under the conditions stipulated by constraint C1 or the interaction described by E2 should be done under the conditions stipulated by constraint C2. The choice we are making here is a committed choice, meaning that if C1 is satisfied then the alternative choice (E2 <-- C2) will not be attempted. 
a(r, X) ::
    E1 <-- C1
    or
    E2 <-- C2
    ...
An example of this pattern is when a buyer wants to send a message to a seller accepting some Offer (received earlier in the definition of the buyer role) if it is acceptable or otherwise it sends a message to the seller rejecting that Offer if it is unacceptable. 
a(buyer, X) ::
    ...
    accept(Offer) => a(seller, Y) <-- acceptable(Offer)
    or
    reject(Offer) => a(seller, Y) <-- unacceptable(Offer)
Since LCC makes committed choices, we know in this example that if acceptable(Offer) is satisfied then the second option (in which the peer attempts to satisfy unacceptable(Offer)) will not be attempted, so if testing unacceptability is not important then we might shorten this example to: 
a(buyer, X) ::
    ...
    accept(Offer) => a(seller, Y) <-- acceptable(Offer)
    or
    reject(Offer) => a(seller, Y)

Pattern 4: Recursion

Often we want an interaction to be controlled by some data structure, for example we might want to have a similar sub-interaction for each of the elements in a list (as in the basic example above). The pattern below describes this. In the pattern r(A) is a role, r, with the data structure as its argument, A. Somewhere within the definition of the of the role appears a constraint, R(A, Ar), that reduces A to some "smaller" structure, Ar. Then the role recurses as r(Ar). Normally there also is an alternative choice for when the data structure does not reduce any further but meets some test, P(A), that it is has reached some terminating state. 
a(r(A), X) ::
    ( ... R(A, Ar) ...
      a(r(Ar), X) )
    or
    ( ... P(A) ... )
One example of using this pattern is an interaction that sends as a message each element, M, from a list [M1,...] to peer p2 in role r2. 
a(r(A), X) ::
    ( M => a(r2, p2) <-- A = [M|Ar] then
      a(r(Ar), X) )
    or
    ( null <-- A = [] )
A second example is an interaction that sends N messages to peer p2, each with the same content, M. Here, N and M are parameters to the role, r. 
a(r(N, M), X) ::
    ( M => a(r2, p2) <-- N > 0 and N1 is N - 1 then
      a(r(N1, M), X) )
    or
    ( null <-- N =< 0 )
Many examples of LCC in use for specifying interactions can be found in the OpenKnowledge publications list.

Programming the OpenKnowledge Kernel

Several interpreters for LCC have been written in different languages (Prolog, Lisp, Java) but the OpenKnowledge kernel is the first attempt to produce a robust kernel system that combines LCC with peer to peer query routing, ontology matching and visualisation. The first publicly available version of this kernel should appear in late Spring 2007 and it will be released as Java open source, so you can develop your own system based on it or contribute to our version. Watch this space for details of how to obtain it and how to contribute to its coding. In the meantime, if you are interested in advance information on its structure and functionality then please read the architectural description and the functionality description.

Building a Better Manual

This manual will change as our work on the LCC language and the OpenKnowledge kernel proceeds. If you have suggestions for improvements to this manual then please mail them to Dave Robertson (dr@inf.ed.ac.uk).