


Next: Using Distance Transform to
Up: Matching Method for Defect
Previous: Matching Method for Defect
The Hausdorff Distance
The basis of our methodology is the median Hausdorff distance which is a
similarity measure between two arbitrary point sets. The classical Hausdorff
distance between two (finite) sets of points, 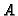 and
and 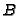 ,
is defined as
,
is defined as
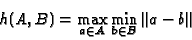 |
(1) |
Here, 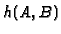 ,
the directed distance from
,
the directed distance from 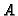 to
to 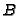 ,
will be small when every point of
,
will be small when every point of 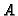 is near some point of
is near some point of 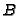 .
This distance is too fragile for practical tasks:
for example, a single point in
.
This distance is too fragile for practical tasks:
for example, a single point in 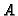 that is far from anything in
that is far from anything in 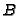 will cause
will cause
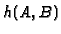 to be large. A natural way to take care of this problem is to
replace equation 1 with
to be large. A natural way to take care of this problem is to
replace equation 1 with
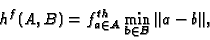 |
(2) |
where
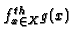 denotes the
denotes the 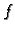 -th quantile value of
-th quantile value of 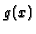 over the set
over the set 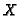 ,
for some value of
,
for some value of 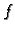 between zero and one.
When
between zero and one.
When 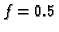 we get the modified median Hausdorff distance
which we use in our method.
we get the modified median Hausdorff distance
which we use in our method.
Let 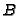 be a point set representing the reference shape,
be a point set representing the reference shape, 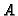 the measured point
set. As already mentioned,
we assume that
the measured point
set. As already mentioned,
we assume that 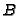 is complete, dense and precise, while
is complete, dense and precise, while 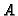 may be incomplete,
sparse and noisy.
may be incomplete,
sparse and noisy. 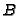 is obtained either analytically, or as the
result of a careful, high-resolution, off-line measurement.
is obtained either analytically, or as the
result of a careful, high-resolution, off-line measurement.



Next: Using Distance Transform to
Up: Matching Method for Defect
Previous: Matching Method for Defect
Dmitry Chetverikov
1998-11-16
![]() and
and ![]() ,
is defined as
,
is defined as
![]() be a point set representing the reference shape,
be a point set representing the reference shape, ![]() the measured point
set. As already mentioned,
we assume that
the measured point
set. As already mentioned,
we assume that ![]() is complete, dense and precise, while
is complete, dense and precise, while ![]() may be incomplete,
sparse and noisy.
may be incomplete,
sparse and noisy. ![]() is obtained either analytically, or as the
result of a careful, high-resolution, off-line measurement.
is obtained either analytically, or as the
result of a careful, high-resolution, off-line measurement.