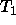 and
and 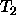 which are to be unified:
which are to be unified:



The way in which Prolog matches two terms is called unification. The idea is similar to that of unification in logic: we have two terms and we want to see if they can be made to represent the same structure. For example, we might have in our database the single Polog clause:
parent(alan, clive).and give the query:
|?- parent(X,Y).We would expect
X to be instantiated to alan
and Y to be instantiated
to clive when the query succeeds. We would say that the term
parent(X,Y) unifies with the term
parent(alan, clive) with X
bound to alan and Y bound to clive.
The unification algorithm in Prolog is roughly this:
df:un
Given two terms 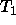 and
and 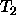 which are to be unified:
which are to be unified:
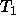 and
and 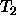 are constants (i.e. atoms or numbers) then if they are
the same succeed. Otherwise fail.
are constants (i.e. atoms or numbers) then if they are
the same succeed. Otherwise fail.
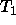 is a variable then instantiate
is a variable then instantiate 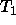 to
to 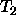 .
.
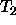 is a variable then instantiate
is a variable then instantiate 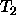 to
to 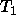 .
.
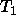 and
and 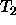 are complex terms with the same arity
(number of arguments), find the principal functor
are complex terms with the same arity
(number of arguments), find the principal functor 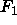 of
of 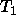 and
principal functor
and
principal functor 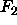 of
of 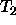 . If these are the same, then take the
ordered set of arguments of
. If these are the same, then take the
ordered set of arguments of 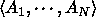 of
of 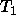 and the ordered set of arguments
and the ordered set of arguments 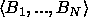 of
of
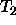 . For each pair of arguments
. For each pair of arguments 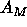 and
and
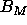 from the same position in the term,
from the same position in the term, 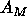 must unify with
must unify with 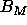 .
.
For example: applying this procedure to unify foo(a,X) with
foo(Y,b) we get:
foo(a,X) and foo(Y,b) are complex terms with the
same arity (2).
foo.
foo(a,X) are a and X.
foo(Y,b) are Y and b.
a and Y must unify , and X and b
must unify.
Y is a variable so we instantiate Y to a.
X is a variable so we instantiate X to b.
foo(a,b).
The built in Prolog operator '=' can be used to unify two terms.
Below are some examples of its use. Annotations are between ** symbols.
| ?- a = a. ** Two identical atoms unify **
yes
| ?- a = b. ** Atoms don't unify if they aren't identical **
no
| ?- X = a. ** Unification instantiates a variable to an atom **
X=a
yes
| ?- X = Y. ** Unification binds two differently named variables **
X=_125451 ** to a single, unique variable name **
Y=_125451
yes
| ?- foo(a,b) = foo(a,b). ** Two identical complex terms unify **
yes
| ?- foo(a,b) = foo(X,Y). ** Two complex terms unify if they are **
X=a ** of the same arity, have the same principal**
Y=b ** functor and their arguments unify **
yes
| ?- foo(a,Y) = foo(X,b). ** Instantiation of variables may occur **
Y=b ** in either of the terms to be unified **
X=a
yes
| ?- foo(a,b) = foo(X,X). ** In this case there is no unification **
no ** because foo(X,X) must have the same **
** 1st and 2nd arguments **
| ?- 2*3+4 = X+Y. ** The term 2*3+4 has principal functor + **
X=2*3 ** and therefore unifies with X+Y with X instantiated**
Y=4 ** to 2*3 and Y instantiated to 4 **
yes
| ?- [a,b,c] = [X,Y,Z]. ** Lists unify just like other terms **
X=a
Y=b
Z=c
yes
| ?- [a,b,c] = [X|Y]. ** Unification using the '|' symbol can be used **
X=a ** to find the head element, X, and tail list, Y, **
Y=[b,c] ** of a list **
yes
| ?- [a,b,c] = [X,Y|Z]. ** Unification on lists doesn't have to be **
X=a ** restricted to finding the first head element **
Y=b ** In this case we find the 1st and 2nd elements **
Z=[c] ** (X and Y) and then the tail list (Z) **
yes
| ?- [a,b,c] = [X,Y,Z|T]. ** This is a similar example but here **
X=a ** the first 3 elements are unified with **
Y=b ** variables X, Y and Z, leaving the **
Z=c ** tail, T, as an empty list [] **
T=[]
yes
| ?- [a,b,c] = [a|[b|[c|[]]]]. ** Prolog is quite happy to unify these **
yes ** because they are just notational **
** variants of the same Prolog term **


