


Next: Coplanar configurations
Up: Unambiguous Pose Determination from
Previous: Absolute orientation
Our goal is to directly get the unique solution
from a redundant polynomial equation system.
Finding the common roots
is equivalent to the determination
of the zero-dimensional variety
generated by the ideal
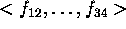 .
We can algebraically get a linear polynomial in generic cases
and in one of
the unknowns
by successive application of Ritt method or pseudo division
[1]
of polynomials over
.
We can algebraically get a linear polynomial in generic cases
and in one of
the unknowns
by successive application of Ritt method or pseudo division
[1]
of polynomials over 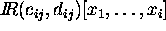 .
This can effectively be done
with any computer algebra system and
will directly give the unique solution of the problem
for general configurations of the points.
However this algebraic method
is almost useless for practical situations
as the successive elimination will ultimately give complicated
coefficients for the final linear polynomial
which compromise
the numerical stability of the solution.
Instead of doing it algebraically,
our goal is to develope a numerical linear method
which indeed gives the unique solution if it does exist.
.
This can effectively be done
with any computer algebra system and
will directly give the unique solution of the problem
for general configurations of the points.
However this algebraic method
is almost useless for practical situations
as the successive elimination will ultimately give complicated
coefficients for the final linear polynomial
which compromise
the numerical stability of the solution.
Instead of doing it algebraically,
our goal is to develope a numerical linear method
which indeed gives the unique solution if it does exist.
For n points,
each pair of points gives a 4th degree polynomial,
we can have
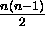 quadratic constraints of type
quadratic constraints of type 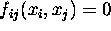 on the n unknown distances
on the n unknown distances 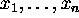 ,
and
,
and
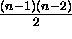 4th degree polynomials of type
4th degree polynomials of type 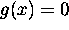 in one variable
in one variable 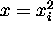 .
.
For n=4,
we obtain three 4th degree polynomials
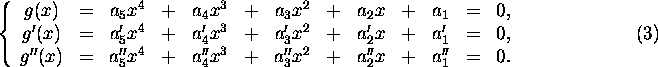
Let the 5-vector 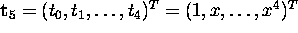 ,
this can be rewritten in matrix form:
,
this can be rewritten in matrix form:
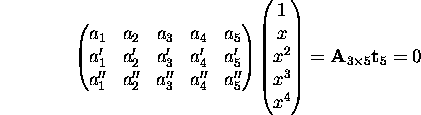
This can be viewed as a homogeneous linear equation system
in 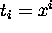 for
for 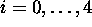 .
Since the matrix
.
Since the matrix 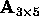 has at most rank
has at most rank 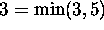 ,
the singular value decomposition
of
,
the singular value decomposition
of 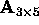 is
is
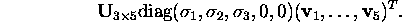
The null space of 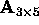 is spanned by the right singular vectors
is spanned by the right singular vectors
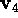 and
and 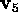 .
Therefore we can construct a
1-dimensional solution space
for
.
Therefore we can construct a
1-dimensional solution space
for 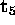 ,
parameterized
by
,
parameterized
by 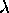 and
and 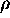 :
:
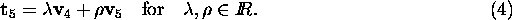
Now consider the nonlinear constraints
among the components of 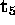 .
It can be easily checked that
.
It can be easily checked that
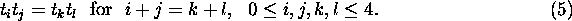
Substituting 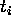 from
(4)
in (5)
gives a homogeneous quadratic equation
in
from
(4)
in (5)
gives a homogeneous quadratic equation
in 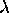 and
and 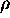 :
:
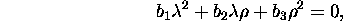
where
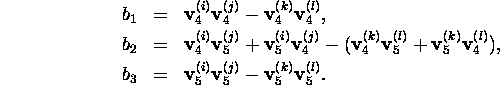
We have 7 such equations for the 7 different values of
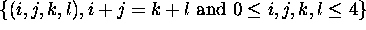 modulo the interchanges of i and j or k and l:
modulo the interchanges of i and j or k and l:
|
(i,j,k,l) |
| (4, 2, 3, 3) |
| (4, 1, 3, 2) |
| (4, 0, 3, 1) |
| (4, 0, 2, 2) |
| (3, 1, 2, 2) |
| (3, 0, 2, 1) |
| (2, 0, 1, 1) |
These 7 quadratic equations can be written in the following
matrix form:
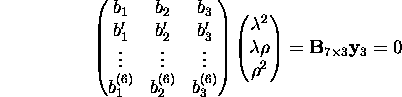
This overdetermined system can
be viewed as linear in
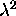 ,
, 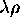 and
and 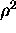 ,
and solved by SVD
as the right singular vector of the smallest singular value
of
,
and solved by SVD
as the right singular vector of the smallest singular value
of 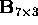 .
It is clear that these 7 equations are linearly
but not algebraically independent.
The constraints
are the algebraic conditions
for
.
It is clear that these 7 equations are linearly
but not algebraically independent.
The constraints
are the algebraic conditions
for 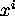 ,
,
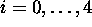 to be a geometric series.
to be a geometric series.
Given the null vector 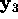 ,
we solve for
,
we solve for
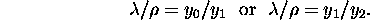
After obtaining the ratio 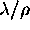 ,
,
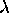 and
and 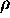 can be determined
using one of the scalar equations of the solution (4),
can be determined
using one of the scalar equations of the solution (4),

Therefore 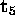 is completely determined.
The final x is taken to be
is completely determined.
The final x is taken to be
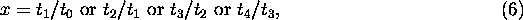
or the average of all these values.
Since 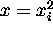 ,
the final positive depth is
,
the final positive depth is 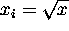 .
.
Hence,
the pose of the calibrated camera
is uniquely determined by 4 point correspondences provided
that the 4 reference points together with
the perspective center of the camera
do not lie in a critical configuration.
The unique solution can be estimated by the linear 4-point algorithm.



Next: Coplanar configurations
Up: Unambiguous Pose Determination from
Previous: Absolute orientation
Bob Fisher
Mon Mar 29 14:15:27 BST 1999
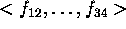 .
We can algebraically get a linear polynomial in generic cases
and in one of
the unknowns
by successive application of Ritt method or pseudo division
[1]
of polynomials over
.
We can algebraically get a linear polynomial in generic cases
and in one of
the unknowns
by successive application of Ritt method or pseudo division
[1]
of polynomials over 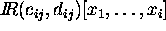 .
This can effectively be done
with any computer algebra system and
will directly give the unique solution of the problem
for general configurations of the points.
However this algebraic method
is almost useless for practical situations
as the successive elimination will ultimately give complicated
coefficients for the final linear polynomial
which compromise
the numerical stability of the solution.
Instead of doing it algebraically,
our goal is to develope a numerical linear method
which indeed gives the unique solution if it does exist.
.
This can effectively be done
with any computer algebra system and
will directly give the unique solution of the problem
for general configurations of the points.
However this algebraic method
is almost useless for practical situations
as the successive elimination will ultimately give complicated
coefficients for the final linear polynomial
which compromise
the numerical stability of the solution.
Instead of doing it algebraically,
our goal is to develope a numerical linear method
which indeed gives the unique solution if it does exist.



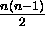 quadratic constraints of type
quadratic constraints of type 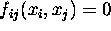 on the n unknown distances
on the n unknown distances 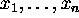 ,
and
,
and
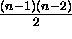 4th degree polynomials of type
4th degree polynomials of type 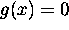 in one variable
in one variable 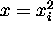 .
.
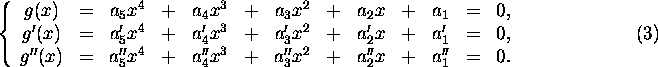
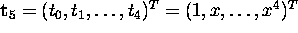 ,
this can be rewritten in matrix form:
,
this can be rewritten in matrix form:
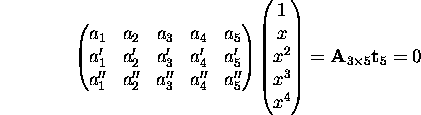
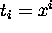 for
for 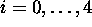 .
Since the matrix
.
Since the matrix 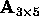 has at most rank
has at most rank 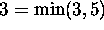 ,
the singular value decomposition
of
,
the singular value decomposition
of 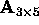 is
is
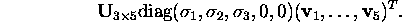
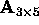 is spanned by the right singular vectors
is spanned by the right singular vectors
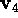 and
and 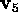 .
Therefore we can construct a
1-dimensional solution space
for
.
Therefore we can construct a
1-dimensional solution space
for 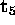 ,
parameterized
by
,
parameterized
by 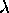 and
and 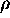 :
:
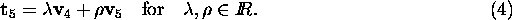
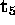 .
It can be easily checked that
.
It can be easily checked that
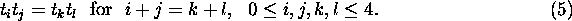
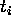 from
(
from
(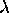 and
and 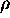 :
:
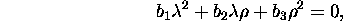
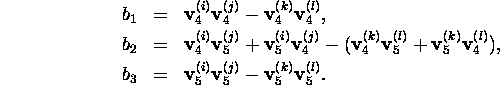
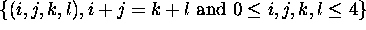 modulo the interchanges of i and j or k and l:
modulo the interchanges of i and j or k and l:
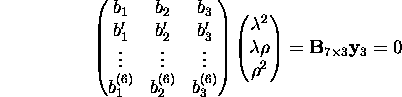
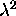 ,
, 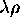 and
and 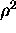 ,
and solved by SVD
as the right singular vector of the smallest singular value
of
,
and solved by SVD
as the right singular vector of the smallest singular value
of 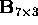 .
It is clear that these 7 equations are linearly
but not algebraically independent.
The constraints
are the algebraic conditions
for
.
It is clear that these 7 equations are linearly
but not algebraically independent.
The constraints
are the algebraic conditions
for 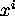 ,
,
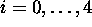 to be a geometric series.
to be a geometric series.
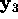 ,
we solve for
,
we solve for
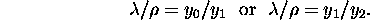
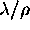 ,
,
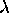 and
and 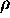 can be determined
using one of the scalar equations of the solution (
can be determined
using one of the scalar equations of the solution (
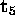 is completely determined.
The final x is taken to be
is completely determined.
The final x is taken to be
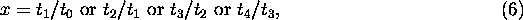
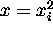 ,
the final positive depth is
,
the final positive depth is 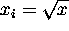 .
.